Amazing Tree Drawing in Circle
So far, we've but been generating drawings with straight lined shapes. This lesson will embrace how nosotros can employ turtle to draw curves and circles. Nosotros'll start past drawing some arcs, and and then build upwards to the point where we can draw a full, 360° circle.
Drawing Arcs #
Fundamental Concept: We tin can describe a line that appears to exist curved by drawing a lot of much shorter lines and rotating but a little flake between each i.
To demonstrate this, allow's look at a program that draws the following xc° arc. This arc covers one quarter of 360°, so this is oftentimes called a "quarter arc".

To figure out how to draw this quarter arc, let'south await at the differences between the beginning position of the turtle (shown below) and the image nosotros're trying to create above.
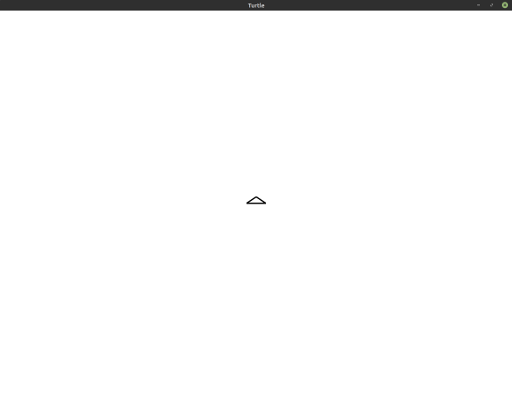
Detect that the turtle appears to go from facing the top of the window to facing the correct. Information technology has moved along a quarter of a circle to become in that location. The programme to generate this arc is as follows:
one 2 3 4 5 6 7 8 ix 10
use turtle :: Turtle ; fn main () { let mut turtle = Turtle :: new (); for _ in 0 .. 90 { turtle .forward ( three.0 ); turtle .right ( 1.0 ); } }
As you can come across, we're doing exactly what we said we would practise earlier: we're cartoon many very small-scale lines and slightly adjusting our angle in every iteration. We instruct the turtle to move 3 steps forward and turn one° to the right every time.
To confirm that this is actually working as described, permit's attempt decreasing the number of iterations and increasing the size of the lines nosotros're cartoon. To describe longer lines, nosotros'll take more than steps. We'll also increase the amount we're turning so that we even so accomplish 90° by the time nosotros're done iterating.
Here's the cartoon that gets created with 3 iterations of the turtle drawing a line for 90 steps and turning thirty° later each line.
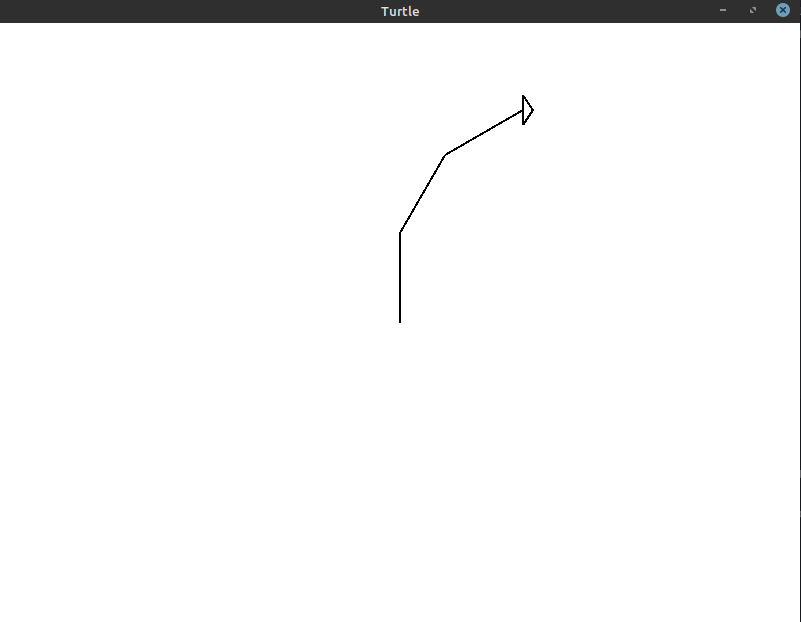
This is the code that generates this image:
1 2 iii four 5 6 7 viii 9 ten 11
apply turtle :: Turtle ; fn main () { let mut turtle = Turtle :: new (); // xxx degrees * 3 = 90 degrees for _ in 0 .. 3 { turtle .forward ( 90.0 ); turtle .right ( thirty.0 ); } }
You tin see that nosotros're still turning the turtle 90° in total, simply the curve doesn't exactly follow the aforementioned circular arc we were getting before. To improve this, permit'due south try v iterations with an 18° turn every fourth dimension:
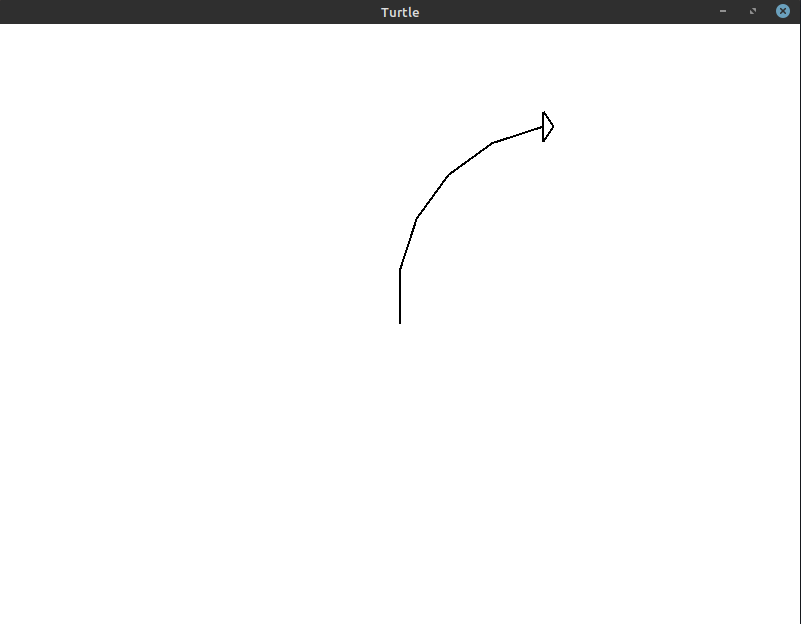
Here's the code that generates that image:
1 two iii four 5 6 7 eight 9 ten 11
use turtle :: Turtle ; fn main () { let mut turtle = Turtle :: new (); // 18 degrees * 5 = 90 degrees for _ in 0 .. five { turtle .forward ( 54.0 ); turtle .right ( 18.0 ); } }
This gets us a niggling closer! If we increase it to nine iterations with a 10° plow, we get the post-obit image:
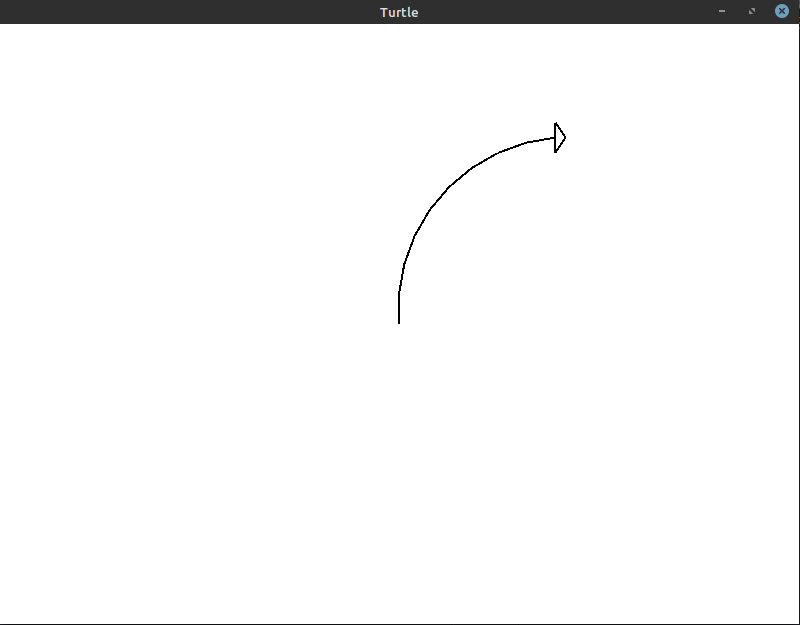
The code for this image:
one two iii 4 5 6 7 8 9 10 11
apply turtle :: Turtle ; fn main () { allow mut turtle = Turtle :: new (); // 10 degrees * 9 = 90 degrees for _ in 0 .. nine { turtle .forwards ( 30.0 ); turtle .correct ( 10.0 ); } }
At this point, information technology's almost indistinguishable. However, if you await close enough, y'all tin still tell that at that place are nine private lines existence fatigued here. Nosotros can make the curve even smoother using 18 iterations with a 5° turn every time:
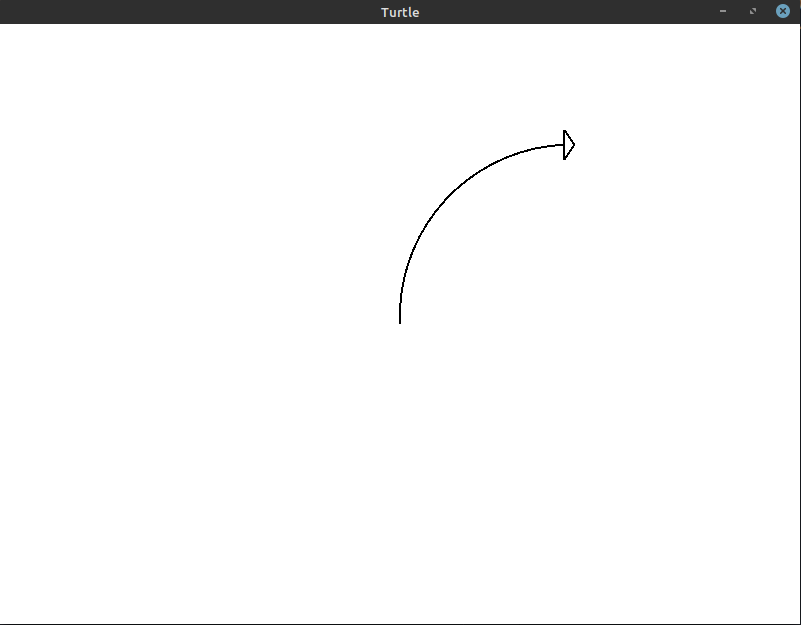
The code for this image:
1 2 3 iv 5 half-dozen 7 8 9 10 11
utilize turtle :: Turtle ; fn main () { let mut turtle = Turtle :: new (); // 5 degrees * xviii = xc degrees for _ in 0 .. 18 { turtle .forward ( fifteen.0 ); turtle .right ( 5.0 ); } }
With this many iterations, we become pretty close. Only to illustrate how much of a difference each increase in iterations makes, hither's a GIF that shows us getting closer and closer to the final quarter arc:

The number of iterations you lot need for your own drawings will depend on the size of the arc you are creating. To be condom, you lot can draw the nigh reliable and authentic arc: 90 iterations with a 1° plough every time:
1 2 three 4 5 six 7 8 ix 10
use turtle :: Turtle ; fn main () { let mut turtle = Turtle :: new (); for _ in 0 .. 90 { turtle .forward ( 3.0 ); turtle .correct ( 1.0 ); } }
This is the aforementioned program from above that gets united states of america the 90° arc nosotros initially set out to create.

Drawing Circles #
Now that we've figured out how to draw a ninety° arc, all we have to do to get a circle is draw four of them (90° * 4 = 360°). Here'south a program you could apply to practise that:
1 2 iii four 5 6 7 8 9 10 xi 12 13
use turtle :: Turtle ; fn main () { allow mut turtle = Turtle :: new (); // Endeavour to avoid programs that expect like this for _ in 0 .. four { for _ in 0 .. ninety { turtle .forward ( iii.0 ); turtle .right ( ane.0 ); } } }
This is probably not the program you want to write! While this program will work, let'south see what we can do if we think through the problem given what we've learned already.
Nosotros know that nosotros want to draw a full circle. A full circle has 360° in it. We know that if we rotate the turtle one° for 90 iterations, we'll draw a quarter arc. Extending that idea, nosotros should try to write a program that performs 360 iterations, rotating the turtle 1° every time.
That'due south how we go to the program beneath:
1 2 three 4 v 6 7 viii 9 10 11 12
use turtle :: Turtle ; fn main () { allow mut turtle = Turtle :: new (); for _ in 0 .. 360 { // Move forward three steps turtle .frontward ( three.0 ); // Rotate to the right (clockwise) by ane degree turtle .right ( 1.0 ); } }
This produces the complete circle shown below:

Exercises #
These exercises are designed to help yous reinforce what you've learned throughout this lesson. All exercises are completely optional. If you get stuck on an exercise, it is totally okay to motion on and come up back to it subsequently.
If you need help, run across the Getting Help section of the guide.
Source: https://turtle.rs/guide/example-circle/
0 Response to "Amazing Tree Drawing in Circle"
Enregistrer un commentaire